关系代数

1.并

相同的合并成一列，不同的并起来

2.减

以R为基准，选择S没有的元组。S中R中没有的不算。

3.乘

4.除

R➗S是R中 ‘包含S在相同属性上投影关系集合’ 的属性

5.连接

自然连接

筛选

只有连接符两边都有的元素才进表

左外连接

连接符左边集合的元素都在，没有对应就是null

右外连接

连接符右边集合的元素都在，没有对应就是null

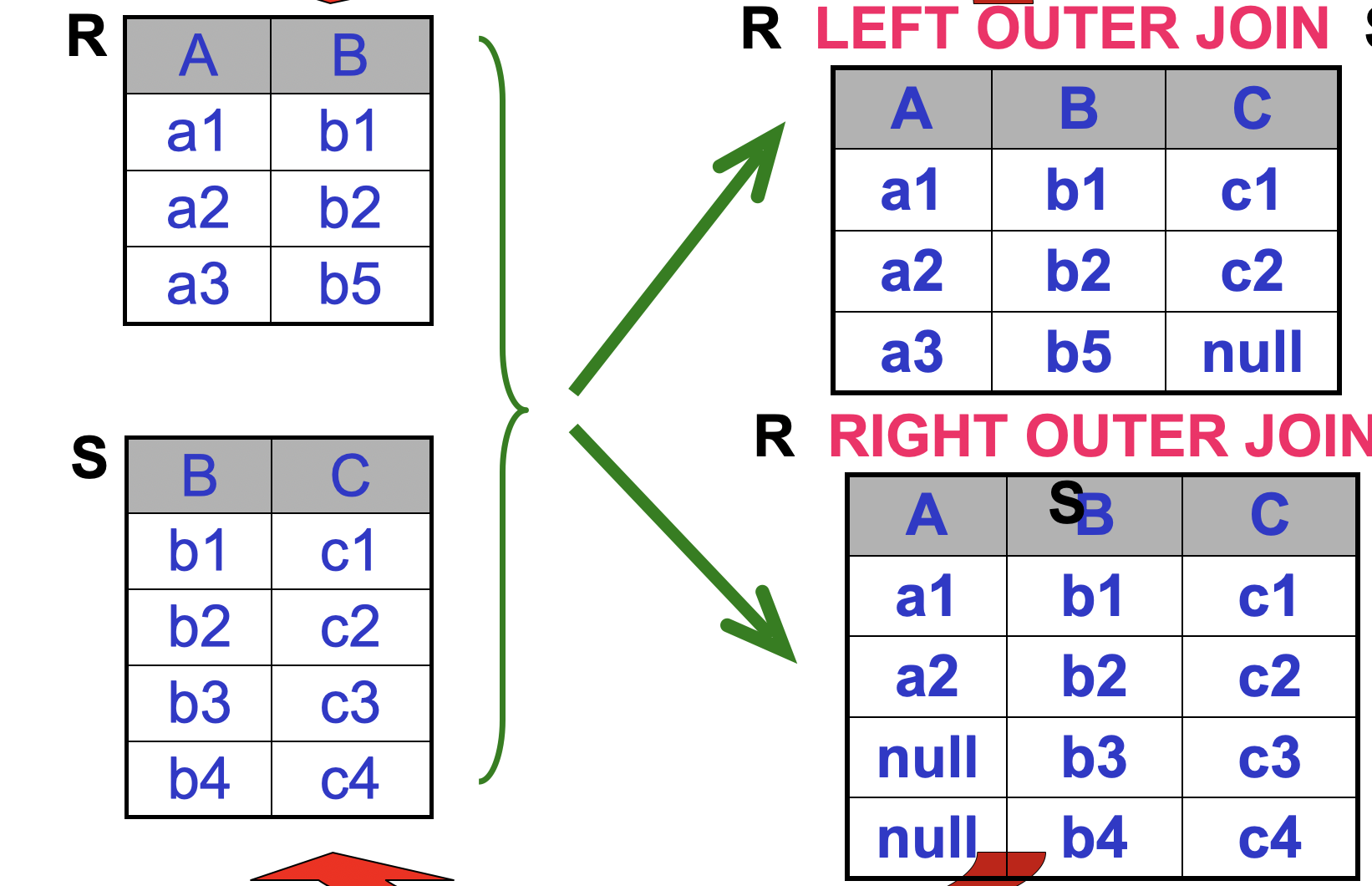
外连接

就是左右连接的并集

$\Theta$连接

$R ∞F_S = (R×S) where F$

6.投影

SQL语法

除

双exist表示：

朴素想法

一种自然的想法是：当一个人的所有技能包含需求的技能时，这个人被选中。试翻译为SQL，

SELECT person
FROM PersonSkill AS PS
GROUP BY person
HAVING PS.skill CONTAINS SKill

可惜这不是一段可以执行的SQL，因为目前SQL不支持集合层面的包含关系判定。

经过观察不难发现，当前SQL支持的所有真假判断（谓词）都定义在元组层面上，这迫使我们将PersonSkill中的person看作分散的个体，每个元组依次独立做出判断。然而，这作用在单个元组上的判断又必须考虑与其同名的其他元组，这让子查询的使用成为必然。最后，由于使某元组为真的谓词必定使其同名元组为真，需要加DISTINCT去重。

综合上述思考，调整SQL语句框架为

1
2
3

SELECT DISTINCT person
FROM PersonSkill AS PS
WHERE <某关于PS.person的谓词(子查询)>

实现减法

我们现在要实现这样一个子查询，根据某人的姓名判断其技能是否满足需求。还是按照最自然的思路，判断某人的技能集是否包含需求集。

取出某人技能集的

1
2
3

SELECT skill
FROM PersonSkill
WHERE person = 某人

需求集

1 2	SELECT skill FROM Skill

记技能集为A，需求集为B，$B ⊆ A$等价于
$ \forall x\in B\rightarrow x\in A$
翻译为SQL

NOT EXISTS (
    SELECT * FROM Skill AS S
    WHERE S.skill NOT IN (
        SELECT skill FROM PersonSkill AS PS
        WHERE PS.person = 某人
    )
)

也可以看作对等价式$B − A = ∅ $的判断，其中NOT EXISTS判定空集，NOT IN实现集合差。

遗憾的是，NOT IN实现集合差只对单列表有效

等价的双EXISTS版本

NOT EXISTS (
    SELECT * FROM Skill AS S
    WHERE NOT EXISTS (
        SELECT * FROM PersonSkill AS PS -- 选A中对应S.skill的元组
        WHERE PS.person = 某人 AND   -- 某人的技能集A中的一个技能
              PS.skill = S.skill    -- 和需求集B中的一个技能相同
    )
)

实现除法

综合上述讨论，

SELECT DISTINCT person
FROM PersonSkill AS PS1
WHERE NOT EXISTS (
    SELECT * FROM Skill AS S    -- WHERE
    WHERE NOT EXISTS (
        SELECT skill FROM PersonSkill AS PS2
        WHERE PS2.person = PS1.person AND
              PS2.skill = S.skill
    )
);

第六章

ER关系图

ER向关系模型转化

函数依赖

寻找表T中的函数依赖

先考虑单个元素决定单个元素
在考虑多个元素的情形

函数依赖集的闭包

给定一个函数依赖集F，它能推导出的所有函数依赖集的集合称为F+

函数依赖集的覆盖

有函数依赖集F，G，若G中的所有函数依赖都能通过F中的函数依赖计算得到，则称F覆盖G

若F覆盖G，同时G覆盖F，则G、F等价

函数依赖集的（最小）覆盖

没有冗余的函数依赖
每一个函数依赖的左边都没有多余的属性

算法：

右边分解成单个属性
去除冗余
- 去掉一个函数依赖
- 如果这个函数依赖左边的属性闭包没变，那么可以去除，否则不能去除
化简左边
- 去掉一个函数依赖左边的一个属性
- 如果去掉这个属性前剩下的属性的属性闭包和去掉后一样，那么能去掉改属性
合并
- 每一列（函数依赖的左边相同）右边乘起来

属性集的闭包

就是一个属性能函数决定的所有属性的集合

算法：

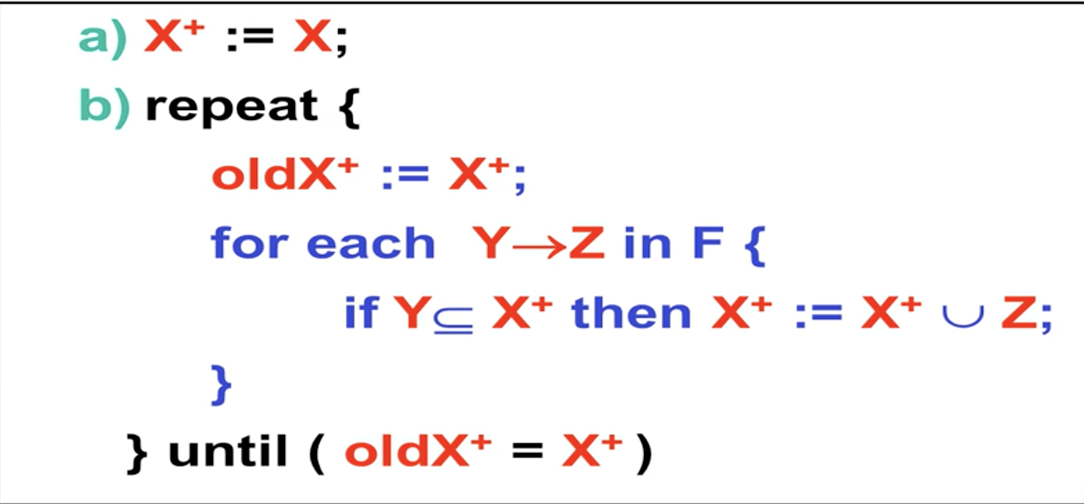
无损连接

定理1（6.7.4）

若$Head(T_1) \bigcap Head(T_2) \rightarrow Head(T_1)$或者

$Head(T_1) \bigcap Head(T_2) \rightarrow Head(T_2)$

则称T1、T2为T的一个无损分解

范式

依赖保持

T上的一个关系F分解为$F1,F_2…$若$F+ ={F1,F_2…}+$则称这个分解有依赖保持性

超键和键（主属性）

发现候选键的算法（做n次）：

令K=Head(T)
删除K中的一个元素A
如果$(K-A)_F^+$包含T中的所有元素
那么可以删去这个元素

主属性就是键的集合K中的单个属性

BCNF范式

判定1：

若函数依赖集合T所有的函数决定都满足超键决定$\rightarrow$一个不在超键中的单一属性。

则称它满足BCNF

判定2：

如果对于任意的函数依赖集F中的依赖$X \rightarrow A$

X是R的超键

则R满足BCNF

3NF 第三范式

第一种判定方法：

如果对于任意的函数依赖集F中的依赖$X \rightarrow A$

X为R的超键
A为R的主属性

满足上述任意一个条件，则称R满足3NF

第二种判定方法：

如果存在$X\rightarrow Y$，Y是单个非主属性，则X必为超键

也就是说：在函数依赖集中，如果单个非主属性一定由超键决定

确定候选键
↓
是否存在非主属性 Y
对主属性部分函数依赖 → 1NF
N↓
非主属性是否 Y
传递依赖于候选键（非主属性是否函数依赖另一个非主属性） → 2NF
N↓
判断所有依赖项的 Y
左边是否全为候选键 → BCNF
N↓
3NF

Suy's page

noteForDataBase